|
En este caso el vértice
A corresponde al polo de la eclíptica Q y el B al polo celeste,
| c
= e |
b=p
/2-b
|
a=p
/2-d |
| |
B=p
/2+a |
A=p
/2-l |
Para
el Sol resulta:
sen a
¤
= tg d
¤
cotg e
tg
a ¤
= tg l
¤ cos
e
sen d
¤ =
sen l ¤
sen e
cos l ¤
= cos a
¤ cos
d ¤
A causa de la precesión
el punto ^ retrocede 50".3 por año.
No varían sin embargo ni b ni e
. Así derivando respecto al tiempo las coordenadas ecuatoriales
y eclípticas resulta, si la unidad de tiempo es el año,
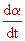 = (cos e + sen e
. sen a . tg d
)
= (cos e + sen e
. sen a . tg d
)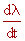
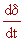 = sen e . cos a
.
= sen e . cos a
. 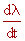
De aquí
que las variaciones debidas a la precesión sean las siguientes:
da
= 3s.07 +1s.34
(sen a tg d
)
d d = 20" cos a
Solamente
cuando un astro esté en el polo de la eclíptica sus coordenadas
permanecerán invariables
( a
= 18h; d = 90 - e
)
Los resultados
anteriores deberían tener en cuenta las perturbaciones producidas
por la nutación, sin embargo las correcciones son muy pequeñas
y pueden ser despreciadas en una primera aproximación.
|