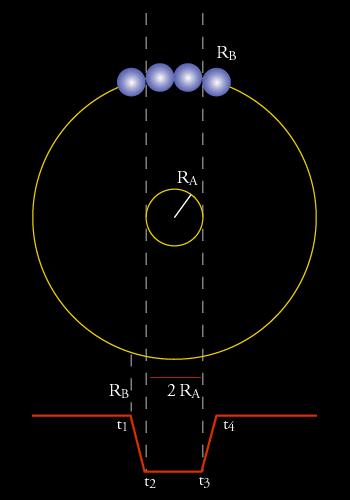
La mejor información se obtiene de los sistemas binarios eclipsantes que son a la vez sistemas espectroscópicos. Todas las binarias eclipsantes son binarias espectroscópicas pero el inverso no es cierto, para ser eclipsante es necesario que la inclinación sea, i @ 90^o . Midiendo la duración de los eclipses y conociendo las velocidades en la órbitas absolutas o la velocidad relativa de una respecto a otra, podemos obtener los radios de cada una de las estrellas. Sea t₁ el instante en e que se produce el primer contacto y t₂ el fin del eclipse, Sí el semieje mayor de la órbita es suficientemente grande comparado con los dos radios estelares y la órbita es casi circular, se puede condiderar de modo aproximado que el objeto más pequeño (B) se mueve perpendicularmente a la línea de observación durante el eclipse. En este intervalo de tiempo el espacio recorrido por B es simplemente

2 R_A + 2 R_B = v (t₄ - t₁)

donde v = v₂ + v₁ es la velocidad relativa de las dos estrellas y v₂ y v₁ son las velocidades de la componente pequeña (B) y grande (A) respectivamente. Análogamente, sí consideramos el tiempo transcurrido entre t₂ y t₃ se puede obtener el espacio recorrido por la estrella pequeña durante la totalidad del eclipse

2 R_A - 2 R_B = v (t₃ - t₂)

Con estas dos ecuaciones obtenemos los radios de ambas estrellas.