|
|
||
|
|
||
|
|
||||||||||
| |
||||||||||
|
|
|||||||||
|
Son aquellas que están muy próximas entre sí para verse separadas pero pueden detectarse por las variaciones periódicas de la velocidad radial, deducidas de los desplazamientos de las líneas de su espectro (Figura 5-6-1). La representación de la velocidad radial frente al tiempo da lugar a la llamada curva de velocidad radial. |
||||||||||
 |
||||||||||
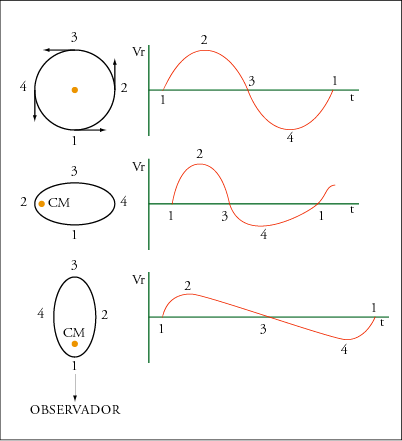
| Figura 5-1-6c Curvas de velocidad radial correspondientes a órbitas de distintos tipos. | ||||||||||
|
La curva de velocidad radial puede dar idea de la forma de la órbita. Para simplificar supongamos la órbita de una estrella alrededor del centro de masas y situada en un plano que contiene a la línea de observación. Consideremos, como ejemplo, tres tipos de órbitas: a) circular; b) elíptica con el semieje mayor perpendicular a la dirección de observación; c) elíptica con el semieje mayor en la dirección de observación. En la Figura 5-1-6c se representan lo tres casos, en las posiciones 1 y 3 el movimiento es perpendicular a la visual y la velocidad radial es cero. Para la órbita circular la curva de velocidad radial es simétrica, es una senusoide. Para una órbita elíptica con el semieje perpendicular al observador, las leyes de Kepler predicen que, la velocidad será mayor en el periastro y en consecuencia tarda menos tiempo en recorrer esta parte de la órbita. La curva de velocidad radial muestra un pico entre los puntos 1, 2 y 3, tarda más tiempo en recorrer de 3 a 4 y volver a llegar a 1. Para una órbita elíptica con su semieje mayor en la dirección de observación, la velocidad cambia rápidamente de negativa a positiva en el punto 1, cerca del periastro. El cambio de velocidad de positiva a negativa en el punto opuesto, 3, es mucho más lenta. La velocidad radial observada, corregida del movimiento de la Tierra, es decir, respecto al Sol, está compuesta de dos términos la velocidad radial del centro de masas que es constante, vcm , más la componente radial de la velocidad orbital, v0 , vr = vcm + v0 es evidente que v0 es la velocidad de la estrella en su órbita absoluta, no en la relativa o verdadera. La estrella describe una órbita cerrada, elíptica o circular, alrededor del centro de masas. Por tanto durante un periódo, la distancia que se mueve en una dirección es igual a la que recorre en la opuesta. Sí calculamos el área encerrada por una curva en un periódo, esto es intrgramos sobre un periódo, y la dividimos en dos partes iguales por una recta, esta línea indica el valor de la velocidad del centro de masas, vcm . En el caso de que ambas componentes del sistema contribuyan al espectro observado, SB2, resultan dos curvas de velocidad radial, una para cada estrella. El análisis de la curva de velocidad permite obtener por los valores de su amplitud, a1 sen i. Donde a1 es el semieje de la órbita absoluta de la primaria e i la inclinación de la órbita, que es el ángulo que forma el plano de la órbita con el plano de referencia o del cielo que es perpendicular a la dirección de observación. Por tanto a1 sen i es la proyección del semieje en un el plano del cielo, perpendicular a la dirección de observación. De la otra curva deducimos para la secundaria a2 sen i. La relación entre las masas de las componentes será ahora M1 a1 sen i = M2 a2 sen i . Sí suponemos las órbitas circulares y que se ven los dos espectros, la velocidad orbital para cada una de las estrellas será v1 = 2p a1 / P v2 = 2p a2 / P dividiendo una por otra v1 / v2 = a1 / a2 = M2 / M1 Aplicando la tercera ley de Kepler y multiplicando los dos miembros de la ecuación por sen3 i a3 sen3 i = (a1 sen i + a2 sen i)3 = P2 (M1 + M2 ) sen3 i ya que a sen i = a1 sen i + a2 sen i Con esta ecuación y con la relación de masas: M1 / M2 = a1 sen i / a2 sen i podemos obtener (M1 sen3 i) y (M2 sen3 i) pero no las masas individuales. Sí sólo se observa el espectro de una componente, la más luminosa o primaria, SB1, la información que se obtiene es mucho menor, se deduce la llamada función de masas. Suponemos que sólo conocemos (a1 sen i) (M1 + M2) P2 = (a1 + a2)3 = a13 (1 + a2 / a1)3 = a13 (1 + M1 / M2)3 (M1 + M2) P2 = a13 (M2 + M1)3 / M23 multiplicamos los dos lados por sen3 i a13 sen3 i / P2 = (M2 sen i)3 /(M1 + M2)2 que es la función de masas de una binaria espectroscópica y lo único que se puede deducir. |
||||||||||