|
|
||
|
|
||
|
|
||||||||||
| |
||||||||||
 |
||||||||||
|
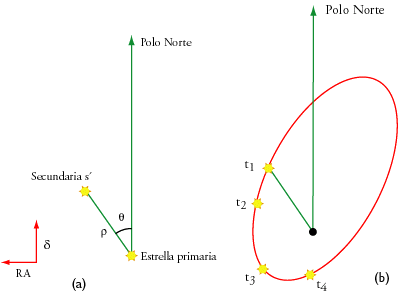
Figura 5-1-2: Binaria visual. a) medida
en un tiempo t de la separación angular
r de las estrellas y del ángulo de posición
q de la secundaria. |
||||||||||
|
Como indicamos en la introducción son aquellas binarias que tienen suficiente separación angular aparente para ser resueltas por un telescopio. Haciendo observaciones regulares se puede determinar su órbita, sus períodos orbitales van de unas pocas decenas de años a cientos de años. Para obtener la órbita se elige una estrella de referencia, normalmente la más brillante de las dos, denominada estrellaprimaria (la más débil es la secundaria). Se observa en un instante t la separación angular r de las estrellas y el ángulo de posición q de la secundaria, que esta definido por el polo norte celeste, la estrella primaria y la secundaria (Figura 5-1-2), siendo positivo en la dirección que aumenta la ascensión recta. La órbita elíptica obtenida a partir de las observaciones recibe el nombre de órbita aparente. La órbita aparente es la proyección de la órbita relativa o verdadera sobre el plano del cielo. Como la órbita relativa es una elipse (dada por las leyes de Kepler) la aparente también lo es aunque de diferente tamaño y forma. La órbita relativa resulta de considerar una estrella fija en el foco y la otra describiendo una elipse alrededor de ella (primera ley de Kepler). Así una vez obtenida observacionalmente la órbita aparente debemos desproyectarla por métodos estándares y obtener la órbita relativa para aplicar la tercera ley de Kepler y así obtener la masa. Las observaciones proporcionan inmediatamente el período, P, en años que será el mismo en la órbita aparente y en la verdadera. También obtenemos el tamaño del semieje mayor, a , en segundos de arco y sí conocemos la distancia, podemos aplicar la tercera ley de Kepler y deducirr la suma de las masas. La tercera ley de Kepler dice: el producto del cuadrado del período por la masa total del sistema es proporcional al cubo del semieje G / 4p2 P2 (M1 + M2 ) = A3 donde G es la constante de gravitación, P el período en años y A el semieje mayor en ua. Sí medimos las masas en masas solares M¤ ,como es usual, esta expresión se simplifica y queda de la forma siguiente: P2 (M1 + M2 ) = A3 para demostrarlo sólo es necesario aplicar la tercera ley a la Tierra y el Sol, donde P = 1 año, A = 1 UA, M1 = M¤ y M2 = MÅ (Tierra) y la masa de la Tierra es despreciable frente a la del Sol G / 4p2 1 (M¤ + MÅ ) = 1 dividiendo la tercera ley por esta ecuación obtenemos la expresión simplificada anterior, siempre que las masas se midan en masas solares. Aplicando esta ecuación, P2 (M1 + M2 ) = A3 , obtenemos la suma de las masas pero como de las observaciones proporcionan el semieje en segundos de arco, a, necesitamos la distancia para obtener el tamaño lineal d (pc) = 1/p" siendo p la paralaje en segundos de arco, A (UA) = a" / p" sustituyendo obtenemos
P2 (M1 + M2 ) = (a"/p")3 Así calculamos la suma de las masas de las dos estrellas. Sí queremos las masas individuales debemos hacer más observaciones. Es necesario obtener la órbita absoluta, es decir, la que recorre cada una de las dos estrellas alrededor del centro de masas del sistema. Para ello hay que conocer las posiciones de ambas estrellas, observando su movimiento respecto a las estrellas muy lejanas del fondo, durante un largo período de tiempo. |
||||||||||
|
|
|||||||||
|
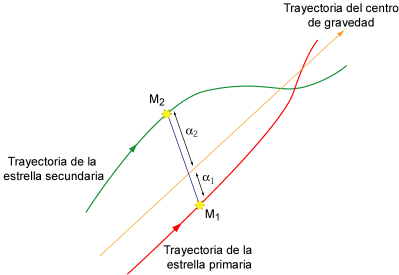
El centro de masas del sistema o centro de gravedad recorre una trayectoria rectilínea, cuando se observa respecto a las débiles estrellas del fondo y las dos componentes del sistema siguen trayectorias curvas con una lenta oscilación alrededor del centro de masas (Figura 5-1-3). |
||||||||||
 |
||||||||||
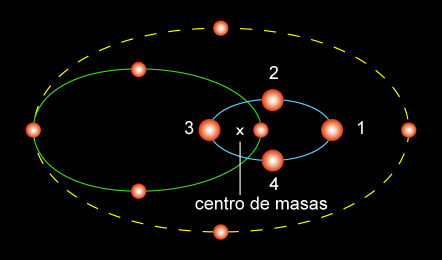
| Figura 5-1-4: Órbitas absolutas respecto al centro de masas. Órbita relativa (a trazos), suponiendo que la estrella de mayor masa permanece fija en el foco. | ||||||||||
|
Con estas observaciones podemos determinar los semiejes mayores de las órbitas absolutas en segundos de arco, a1" y a2", además, se verifica que el semieje de la órbita relativa a" es la suma de los semiejes de las órbitas absolutas a" = a1" + a2" (Figura 5-1-4) y por el teorema del centro de masas: M1 a1" = M2 a2" M1 / M2 = a2" / a1" con esta ecuación y la tercera ley de Kepler: P2 (M1 + M2 ) = (a"/p")3 podemos obtener las masas individuales de cada estrella. Las masas típicas obtenidas de las binarias visuales van de 0.1 a 20 M¤. |
||||||||||