• Homogeneidad e isotropía
• Geometría
• Dinámica del Universo en expansión

El estudio de las propiedades del universo en expansión está enmascarado por los distintos movimientos de la Tierra y el Sol y también por los correspondientes a la Galaxia como miembro del Grupo Local y de éste en el supercúmulo de Virgo. Las observaciones corregidas de todos estos movimientos son las mismas que obtendría un observador comovil.

La posición de un objeto particular, por ejemplo de una galaxia, queda fijada por unas coordenadas comoviles que no cambian durante la expansión o hipotética contracción del universo. Para obtener las distancia entre dos galaxias deberemos multiplicar estas coordenadas por algún factor de escala R(t). Así, el intervalo entre dos sucesos separados en el espacio por dx, dy, dz y en el tiempo por dt es

ds² = c² dt² - R²(t) du²

du² = dx² + dy² +dz² representa la distancia entre dos puntos en una métrica espacial euclidea, ordinaria. La parte espacial del intervalo, cdt, es el tiempo transcurrido entre dos sucesos que ocurren en el mismo punto ( dx = dy = dz = 0 ). La distancia entre dos puntos fijos del espacio es proporcional a R (t) y el volumen a R³(t).

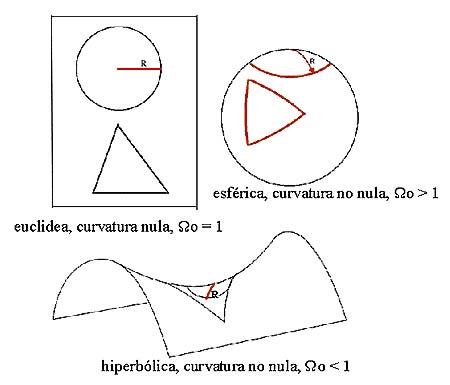
Figura 8-1-4: Geometria esférica, hiperbólica y euclidea

Como a priori no conocemos la geometría del universo, la métrica ha de ser lo más general posible y además debe ser consistente con las propiedades de un universo homogéneo e isótropo. Por ello viene dada por la relación,

donde r, q y F son las coordenadas comoviles. La curvatura del espacio viene representada por k que define los diferentes tipos de geometría. Por ejemplo, k = 0, espacio euclideo ordinario, plano, y la métrica esta expresada en coordenadas esféricas; k = 1 curvatura positiva, espacio esférico no euclideo; k = -1 curvatura negativa, espacio hiperbólico no euclideo ( figura 8-1-4 ). Para caracterizarlas de modo elemental damos algunas de sus propiedades: la suma de los ángulos de un triángulo, S, la longitud de una circunferencia, L, y el volumen de una esfera, V ,

De manera que en un volumen suficientemente grande del universo el número de galaxias es menor en un universo esférico que en otro euclideo. El hiperbólico será el que contenga más galaxias de los tres. Estos resultados podrían en principio servir para discriminar entre los distintos modelos, desgraciadamente las diferencias sólo son perceptibles a muy gran escala, por lo que es muy probable que los objetos distantes que sean poco brillantes queden excluidos del recuento.

La tasa de expansión, esto es la variación relativa del tamaño del universo con el tiempo es

= H(t)

particularizando para el instante actual, t = t₀, resulta la constante de Hubble,

Ho = H(t₀ ) =

La tasa de aceleración o frenado de la expansión del universo viene dada por la expresión,

es conveniente a efectos de su utilización práctica multiplicar la relación anterior por R(t), resultando así el parámetro de deceleración, q, que carece de dimensiones. Particularizando para el instante actual, resulta

q_o = =

La longitud de onda de un fotón en el instante de su emisión, l (te), es proporcional a R(te). De manera que

= 1+z

Como el universo está en expansión, R(to) es mayor que R(te) y consiguientemente l(to) > l (te). Por tanto la longitud de onda de la señal luminosa emitida por una fuente distante aumenta en un valor de 1+z, en su camino hacia el observador. Así, el desplazamiento al rojo que presentan todas las galaxias distantes es consecuencia de la expansión del universo como un todo.